Es importante que sepamos cómo comparar préstamos antes de solicitar uno. Tanto la tasa de interés, la Tasa Nominal Anual (TNA), la Tasa Efectiva Anual (TEA) y el Costo Financiero Total (CFT) son conceptos que parecen difíciles de entender. Tranqui, en este artículo te contamos qué significa cada uno y qué tenés que mirar a la hora de comparar préstamos.
Qué es la tasa de interés
Si queremos sacar un préstamo personal debemos prestar especial atención a la tasa de interés.
La tasa de interés es el precio que la entidad financiera nos cobra por prestarnos plata. También podemos definirla al revés, como el costo que debemos pagarle a quien nos presta plata (por ejemplo, un banco o una fintech). Generalmente lo expresamos como porcentaje.

La cantidad de interés que pagaremos por un préstamo dependerá de cuatro factores:
- La cantidad de plata que pedimos prestada: Cuanto más pidamos prestado, más intereses pagaremos, ya que estos se calculan como un porcentaje del monto del préstamo.
- Por cuánto tiempo se pide prestado: Pedir prestado también costará más cuanto mayor sea la duración del préstamo, ya que hay más tiempo para que se acumulen los intereses.
- Con qué frecuencia se calcula el interés (diario, mensual, anual, etc.): Cuanto más seguido se calcule el interés (también llamado capitalización), mayor será la cantidad de plata que pagaremos al final. Por ejemplo, un 40% de interés calculado mensualmente resultará en más intereses que el 40% calculado anualmente. Detallaremos en profundidad este tema más adelante.
- La tasa de interés: Cuanto más alta sea la tasa de interés, más interés pagaremos. Una tasa de interés del 10% resultará en más interés que una tasa del 5%. El problema es que cuando comparamos tasas de interés, debemos asegurarnos de comparar manzanas con manzanas. ¿Por qué decimos esto? Porque como acabamos de ver, el 40% de interés mensual es diferente al 40% anual.
Cuando hablamos de tasa de interés, no es lo mismo la Tasa Nominal Anual (TNA) y la Tasa Efectiva Anual (TEA). Tampoco es lo mismo el Costo Financiero Total (CFT) y las otras siglas que aparecen como letra chica en los folletos de los préstamos. Veamos en detalle cada una.
Tasa Nominal Anual (TNA)
La Tasa Nominal Anual de un préstamo (TNA) es el porcentaje de interés que pagaremos por la plata que nos prestaron, en un plazo de un año y suponiendo que los intereses se calculan una sola vez y la devolución se hace toda junta.
Veamos un ejemplo: si en enero 2021 solicitamos un préstamo de $10.000 con una TNA del 40%, en enero 2022 (al año) deberíamos devolver esos $10.000 más $4.000 en concepto de intereses, todo junto y en un único pago. Ya que $4.000 es el 40% de $10.000 y en este ejemplo solamente calculamos intereses una sola vez (al final el préstamo).
La TNA es una tasa contractual que sirve para darnos una referencia básica, pero no nos es útil para comparar préstamos. Esto es así porque en la práctica no se suelen calcular intereses en un único pago anual, sino que suelen calcularse varias veces a lo largo de un año.
Dependiendo de la frecuencia con la que se calculan los intereses -ya sea anual (1 vez), semestral (2 veces), trimestral (4 veces), mensual (12 veces), etc-, el valor del préstamo va a cambiar.
Vamos a tener que buscar una forma para poder equilibrar nuestras tasas y poder compararlas. Y la forma más sencilla de hacerlo es con la Tasa Efectiva Anual (TEA).
Tasa Efectiva Anual (TEA)
La Tasa Efectiva Anual (TEA) está formada por la Tasa Nominal Anual (TNA), que mencionamos más arriba, pero teniendo en cuenta la frecuencia con la que se calcula (capitaliza) el interés.
Sigamos con el ejemplo anterior de pedir un préstamo de $10.000 en enero 2021 a una TNA del 40%, pero ahora suponiendo que los intereses se calculan mes a mes. Esto significa que al final de cada mes, el interés se calculará en función de la cantidad de plata pendiente a ese momento.
- Después del primer mes, al finalizar enero, deberíamos aproximadamente $10.333. Ese importe corresponde al valor de la plata que pedimos prestada más los intereses del mes. Calcularemos estos intereses como $10.000 que pedimos prestado x (40% de tasa nominal anual dividida por 12 meses).
- Después del segundo mes, al finalizar febrero, deberíamos $10.677. El interés del mes 2 se obtendrá de la siguiente manera: $10.333 que debíamos en enero x (40% de tasa nominal anual dividida por 12 meses).
- Después del tercer mes, en marzo, deberíamos $11.033.
Y así sucesivamente.
Si hacemos esta misma cuenta mes a mes, vamos a obtener estos valores:

Al finalizar el último mes (al mes 12) lo que estaríamos adeudando sería $14.821,26. Este valor está compuesto por los $10.000 que nos prestaron más $4.821,26 en concepto de intereses.
En este ejemplo, si bien fuimos calculando intereses mes a mes con una Tasa Nominal Anual del 40%, en verdad, al final del período, el interés que “efectivamente” pagaremos es $4.821,26 (o sea, el 48,21% del valor inicial del préstamo). Esto sucede porque mes a mes fuimos calculando intereses sobre otros intereses. Ese 48,21% que terminamos pagando en concepto de intereses es lo que llamamos Tasa Efectiva Anual (TEA).
Vale aclarar que la tabla anterior no dice nada sobre la forma en la que devolveremos el préstamo, sino simplemente cómo calcular los intereses al final del período. Para conocer la forma de devolución del préstamo, tenemos que tener en cuenta el sistema de amortización.
Veamos cuánto varía lo que tenemos que pagar al final del mes 12 si pedimos un préstamo de $10.000 con una TNA del 40% pero con distinta frecuencia con la que se calcula el interés.
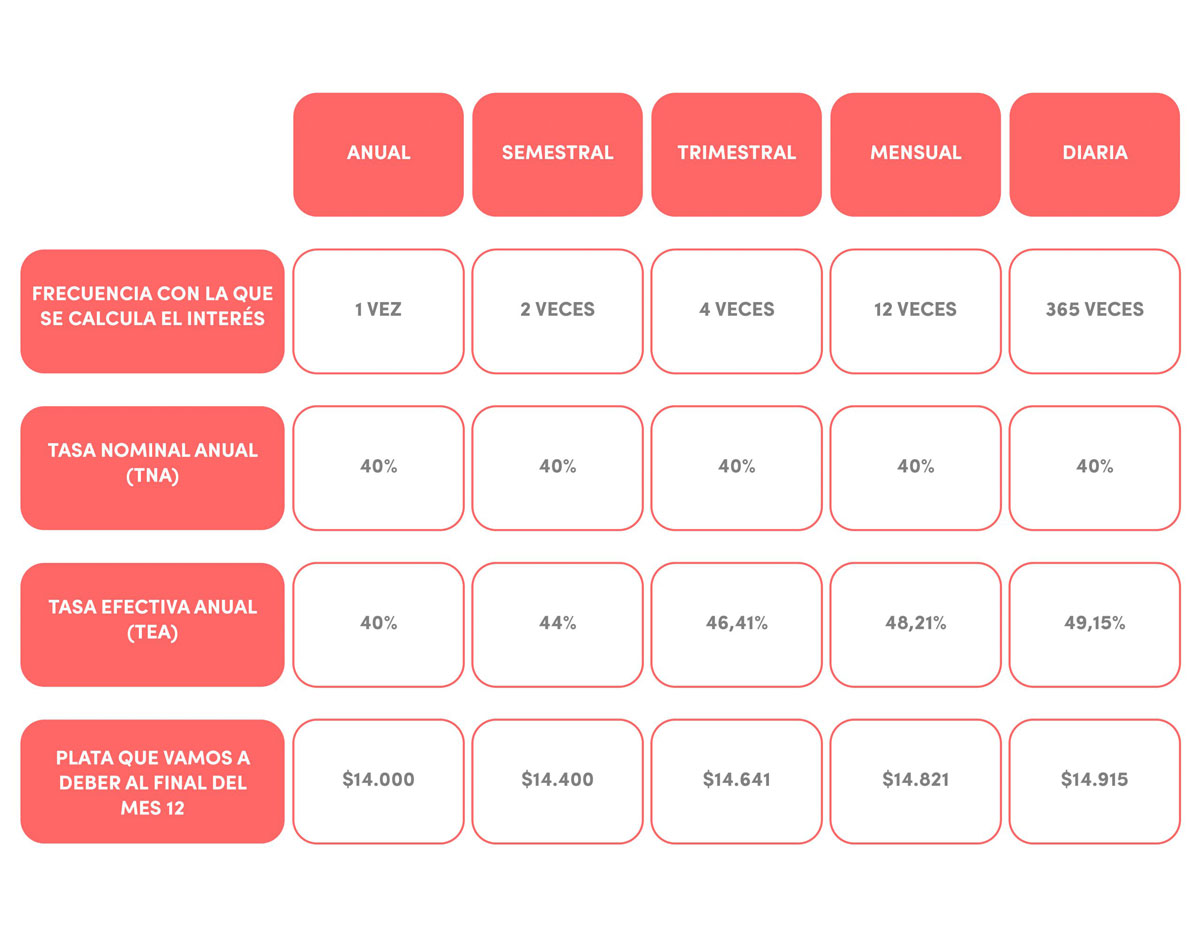
Cuanto más frecuentemente se calcula o capitaliza el interés, más interés se pagará. La Tasa Efectiva Anual (TEA) nos simplifica la forma en la que podemos calcular cuánta plata “efectivamente” vamos a pagar al finalizar nuestro préstamo.
Recapitulando: como contempla la frecuencia con la que se capitalizan los intereses, la TEA permite comparar préstamos con distintas características, siempre que no existan otros costos.
Costo Financiero Total (CFT)
Generalmente, quienes prestan plata no sólo cobran una tasa de interés, también cobran comisiones y otros gastos asociados al préstamo. Esos pueden ser los gastos de apertura y mantenimiento de la cuenta, el costo de cancelación, entre otros.
Esto es lo que se conoce como Costo Financiero Total (CFT), e incluye la tasa de interés más las comisiones y los gastos que se aplican al préstamo. El CFT refleja el monto íntegro que vamos a pagar, porque, además de la tasa, también puede incluir los costos administrativos, operativos, seguros, impuestos e IVA.
Podríamos resumir que el Costo Financiero Total (CFT) = TEA + comisiones + gastos
La normativa respecto de cómo las entidades financieras tienen que exponer el CFT, tanto en folletos como publicidades, cambió a lo largo del tiempo. Actualmente en Argentina es obligatorio por norma expresar el Costo Financiero Total Efectivo Anual con IVA (CFTEA c/IVA), en porcentaje y con dos decimales.
Cuando veamos una publicidad en vía pública o en YouTube sobre préstamos, vamos a poder distinguir bien grande el CFTEA c/IVA. El Banco Central de la República Argentina indica que debe colocarse en una tipografía en color destacado, de idéntica fuente y de tamaño al menos cinco veces mayor al que se utilice para informar el nivel de la Tasa Nominal Anual (TNA).
¿Cómo comparar préstamos cuando tienen una duración menor a un año?
Como ya mencionamos, por normativa del BCRA, los préstamos deben expresar el valor del CFTEA c/IVA. Este costo lo que supone es que el período de tiempo de duración del préstamo va a ser de un año. Sin embargo, existen casos donde los préstamos tienen una duración menor a ese tiempo. Un ejemplo es el producto cuotificaciones al que accedés desde Ualá. Este producto permite pasar a cuotas un consumo que ya realizamos y tienen la particularidad de ser créditos de montos chicos (menores a $5.000) y de corto tiempo de devolución (1 mes, 3 meses o 5 meses).
Como el tiempo de duración es más corto que un año, en estos casos lo que tenemos que hacer es contemplar el CFT solamente por la duración del préstamo.
Supongamos que la semana pasada compramos una remera por $1.200 y hoy necesitamos esa plata nuevamente. Como el producto cuotificaciones nos otorga la plata en el momento y nos da la opción de devolverlo al poco tiempo, estamos pensando utilizarlo. Si elegimos la opción de devolución al mes, nos aparecerá una información similar a esta:

A primera vista ese 128,52% de CFT puede llamarnos la atención. Sin embargo, tenemos que recordar que ese valor es suponiendo que devolveremos el préstamo dentro de un año y nosotros lo vamos a devolver mucho antes. Al finalizar el préstamo, al mes, el valor total de CFT que habremos pagado será solamente de $95,96. En total terminaríamos devolviendo $1.295,96 ($1.200 que nos prestaron y $95,96 por CFT).
Y entonces, cómo comparar préstamos
El CFT es una herramienta adecuada para comparar préstamos de diferentes entidades, siempre que lo haga la misma persona y las ofertas tengan idéntica o similar estructura. Con “estructura” nos referimos a la cantidad de plata que solicitamos, a la duración del préstamo y a las garantías que ofrecen.
El CFT no es muy recomendado para comparar ofertas para diferentes personas y/o ofertas con diferentes estructuras. Por ejemplo comparar un préstamo de dos años de duración con una cuotificación que devolveremos dentro de un mes. En esos casos deben ponderarse cuidadosamente las diferencias que puedan existir entre las alternativas y evaluar el impacto de ellas en el CFT.



