¿Qué es la regla del 72?
La regla del 72 es una fórmula simple que nos permite estimar aproximadamente cuánto tiempo tardará en duplicarse una inversión, teniendo en cuenta el interés o rendimiento que proyectemos. Eso no es todo, también nos posibilita proyectar cuánto tardará nuestra plata en perder la mitad de su valor debido al aumento sostenido de los precios (inflación).
En otras palabras, la regla del 72 nos permite obtener una buena estimación de cuánto tiempo tomará duplicar o reducir a la mitad nuestra plata, sin la necesidad de una calculadora científica o tablas matemáticas complejas.
Veamos cómo funciona.
¿Cómo es su fórmula?
La fórmula de la regla del 72 es muy sencilla. Para calcular el tiempo que tardaremos en duplicar una inversión, deberemos dividir el 72 por la tasa de interés.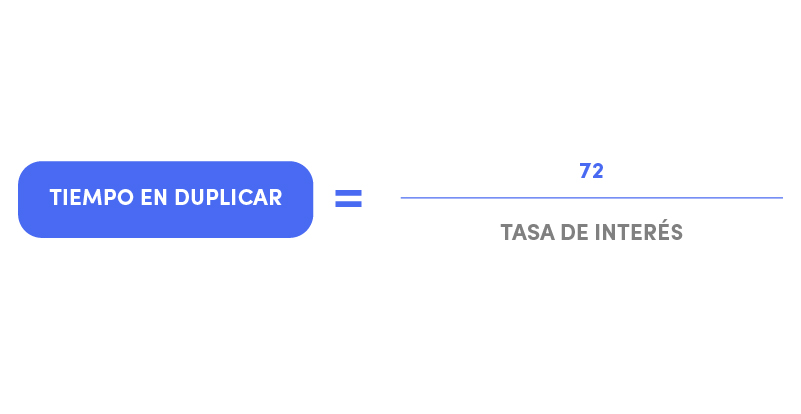 Veamos un ejemplo:
Veamos un ejemplo:
Si proyectamos una inversión que nos de una tasa de interés del 9% anual, para saber en qué momento habremos logrado duplicar nuestra plata tendremos que dividir 72 sobre la tasa de interés. En este caso, al dividir 72 / 9 (la tasa de interés anual) nos da como resultado 8 años.
Tiempo en duplicar = 72 / 9
Tiempo en duplicar = 8
Otros usos para la regla del 72
La regla del 72 también nos permite calcular cómo podría deteriorarse el poder de compra de nuestra plata producto de la inflación. En este caso, la fórmula también es muy sencilla.
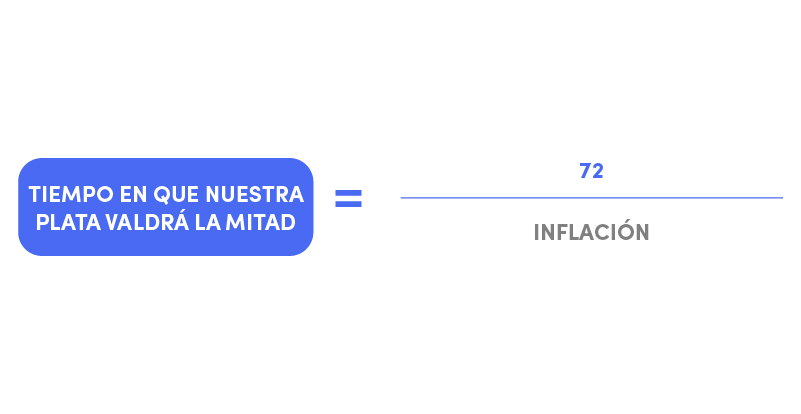
Acá también podemos verlo con un ejemplo:
Si las cosas que necesitamos para vivir aumentan 8% año a año, entonces tomando el 72 y dividiéndolo por 8 tendremos el resultado. Con ese nivel de aumento de precios anual, nuestra plata podrá comprar apenas la mitad de lo que nos permite comprar hoy en aproximadamente 9 años (72/8). Por otro lado, si las cosas aumentan 6% anual, nuestra plata perdería la mitad de su valor en 12 años (72/6).
La regla del 72 en la vida real
Ya conocemos la fórmula de la regla del 72 y qué cosas nos permite estimar. Ahora bien, haciendo una pequeña modificación, también podremos calcular cuánto debería obtener de intereses de una inversión para tener el doble de plata en una determinada cantidad de años.
En nuestra fórmula original, podemos reemplazar “tiempo para duplicar” por “tasa de interés” y calcular el rendimiento necesario que precisamos para duplicar en determinada cantidad de años que queramos.
Fórmula original: Tiempo para duplicar = 72 / Tasa de interés
Reemplazando los términos nos queda qué: Tasa de interés = 72 / Tiempo para duplicar
Entonces, podemos elegir el tiempo en que quisiéramos duplicar nuestra plata y calcular la tasa de interés necesaria. Por ejemplo, 10 años.
Tasa de interés = 72 / 10
Tasa de interés = 7,2
Esto significa que si logramos obtener un rendimiento de 7,2% anual, en 10 años tendremos el doble de lo que hoy tenemos.
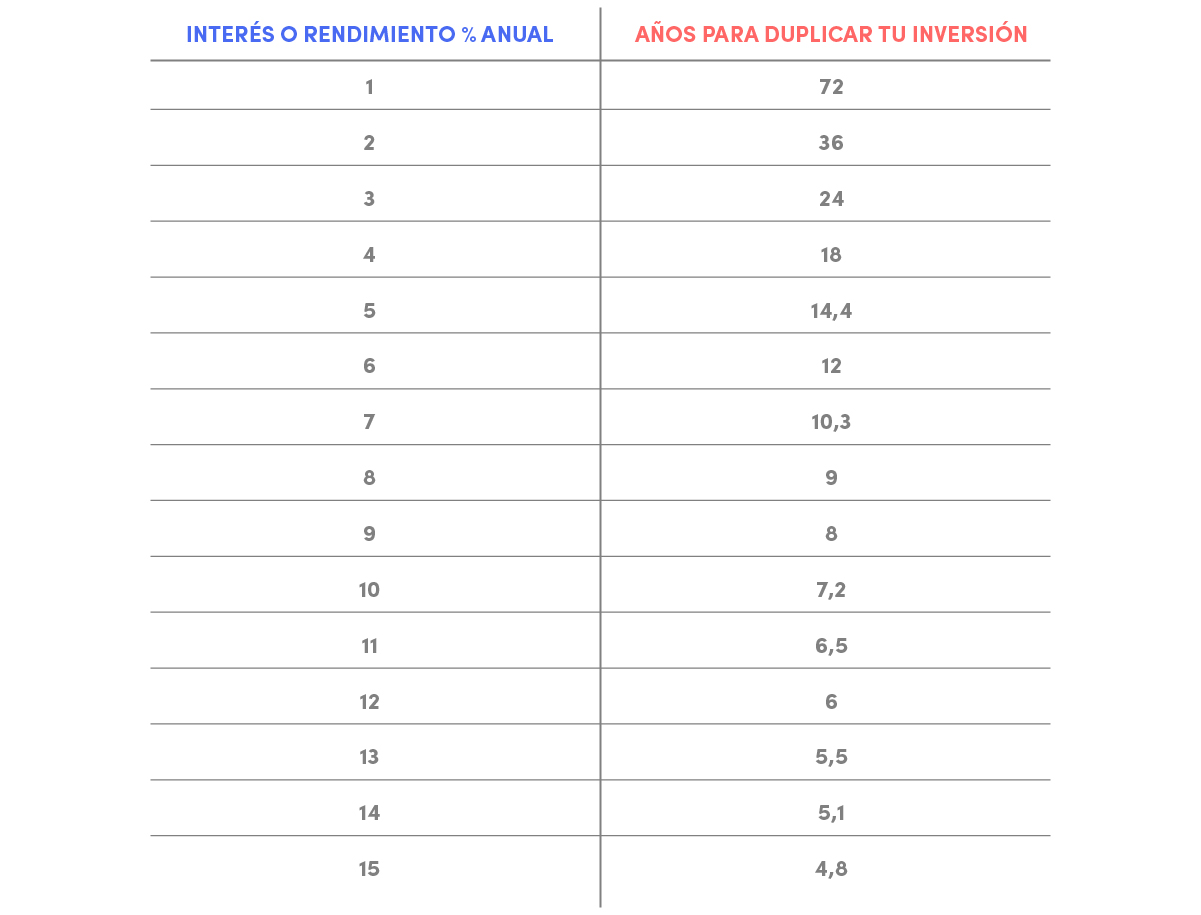
A continuación dejamos una tabla en la que se puede ver fácilmente el tiempo que tardaríamos en duplicar nuestra plata según el interés o rendimiento que logremos obtener por año.
¿Quién popularizó esta regla?
La regla del 72 fue publicada por primera vez en 1494 por Luca Pacioli, un fraile y matemático italiano del renacimiento. Pacioli resumió los conocimientos matemáticos alcanzados hasta el momento en su obra “Summa de Arithmetica” (1494). Se lo considera el primer manual de contabilidad de la historia. En la actualidad se sigue usando su sistema contabilidad de partida doble, aunque no fue inventado por él.
Pacioli estudió a fondo las escuelas del mundo islámico e indio y se cree que la fórmula de la regla del 72 podría proceder de allí.